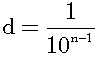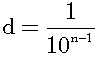The significance of Zeno's Paradoxes
Introduction
Zeno of Elea was a Greek philosopher about 2500 years ago. He is famous for his paradoxes. Most of his writings were lost, but we can know his paradoxes through Aristotle's writings. Four paradoxes were reviewed in Aristotle's Physics. The value of them has not been tarnished since ancient Greek times. Rather, the importance of them is increasing in the digital era. We shall discuss two paradoxes of them:
Achilles and the Tortoise,
the arrow paradox.
Achilles Cannot Catch up the Tortoise
In
physics Ⅵ, Aristotle says "The first asserts the non-existence of motion on the ground that that which is in locomotion must arrive at the half-way stage before it arrives at the goal." This paradox is called the dichotomy. It is similar to next paradox.
Aristotle says "The second is the so-called ‘Achilles’, and it amounts to this, that in a race the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead." These two paradoxes are isomorphic. We shall consider only Achilles and the Tortoise.
Suppose that Achilles is ten times as fast as the Tortoise and the Tortoise starts ahead 10 meters. When Achilles reaches Tortoise's start point, the Tortoise has run 1 meter. Next, Achilles runs 1 meter, the tortoise runs 0.1 meter. Next, Achilles runs 0.1 meter, the Tortoise runs 0.01 meter, and so on. Next equation represents the distance between Achilles and the Tortoise, when Achilles reaches n times where the Tortoise has been.
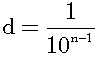
This paradox is the infinite loop. In "
What is infinity?", I describe that an infinite loop cannot reach infinity. If we assume that d does not equal zero for n=k, then d does not equal zero for n=k+1. According to mathematical induction, d will never reach zero. That is, Achilles will never catch up the Tortoise.
Space is not Continuous
Zeno does not claim that Achilles cannot catch up the Tortoise, but he claims that if space were continuous, Achilles could not overtake the Tortoise. That is, if Achilles competed with the Tortoise in a true Euclidean space, he could not win. However, Achilles will easily pass the Tortoise in the real competition. This means that space is not continuous in the real world.
Actually, the difference between Achilles and the Tortoise cannot be strictly determined according to the
uncertainty principle. In 1927,
Heisenberg stated "The more precisely the position is determined, the less precisely the momentum is known in this instant, and vice versa." In subatomic scale, the difference between Achilles and the Tortoise will become undecidable. If they still compete more, it will be impossible to decide which is a front-runner. This means that we cannot regard space as a true Euclidean space. That is, space is not continuous.
The Arrow Paradox
Aristotle says "Zeno’s reasoning, however, is fallacious, when he says that if everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless." Figure 1 shows the movement of an arrow.
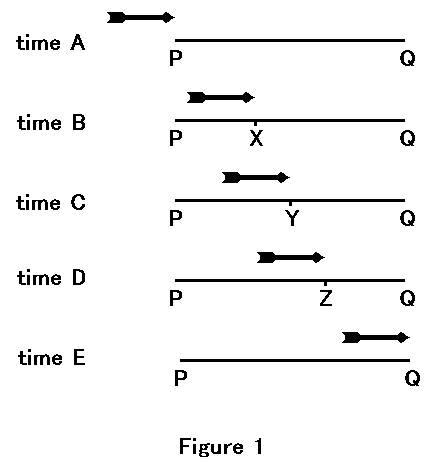
Time A, time B, time C, time D and time E represent instants. Line PQ represents the distance and each picture of the arrow represents the location of the arrow at each instant. At the time A, the tip of the arrow is at the point P. It flies toward the point Q. If our eyes could capture it at an instant, we could see it at the point X, the point Y and the point Z. However, our eyes cannot capture it completely. Even if we could use the highest-performance camera, we could not see the picture of the resting arrow. No matter how fast the shutter speed is, a little blurring remains. How can we completely freeze the arrow?
Our Brain Creates an Instant and a Motion
If we stopped time, we could easily recognize an instant. However, time does not stop but constantly passes. Furthermore, our eyes are far inferior to a
high-speed camera to capture an instant. Of course, it cannot catch a true instant. Why do we have the concept of an instant? The answer is that our brain makes still images. Our eyes must collect enough light from the visual field to make a still image. This task takes a certain time. However, we regard a still image as capturing an instant. That is, we cannot perceive an instant, but our brain creates a still image like catching an instant.
Furthermore,
Donald Hoffman says that your brain constructs the motion that you see. In
chapter six of Visual Intelligence, he shows many examples, so that you can see how your brain creates motions. He describes as follows:
When you watch a movie at the theater, what the projector show is a bunch of still pictures, one after the other. Each second, projector shows you twenty-four different still pictures on and off three times, for a total of seventy-two flashes per second. In between flashes the screen is dark. Indeed, much of your time in the theater, while watching a movie, is spent before a blank screen.
That's what you're given by the projector. But it's not what you see. What you see, of course, is what your visual intelligence constructs.
That is, our brain creates a continuous motion picture from discrete frames. Especially,
visual area 5 is crucial for the perception of the motion. If this area is damaged by a disease, the patient cannot see the motion (1,2). In 1983, James Zihr reported the patient's complaint:
The visual disorder complained of by the patient was a loss of movement vision in all three dimensions. She has difficulty, for example, in pouring tea or coffee into a cup because the fluid appeared to be frozen, like a glacier. In addition, she could not stop pouring at the right time since she was unable to perceive the movement in the cup (or a pot) when the fluid rose.
Thus, our brain creates the continuous motion. Accordingly, we have no choice but to regard time and space as continuous. In conclusion, continuity is created by our brain.
The Simulation of the Motion
Because our
kinetic visual acuity is limited, our brain makes the motion to compensate. For example, the uniform linear motion is the simplest motion. As I show in
The Motion and the Differential Calculus, our brain can make it from only two still pictures of an object. However, if a motion of an object can be modeled by it, we can calculate the movement distance of the object from the travel time. Figure 2 shows the distance-time graph of it.
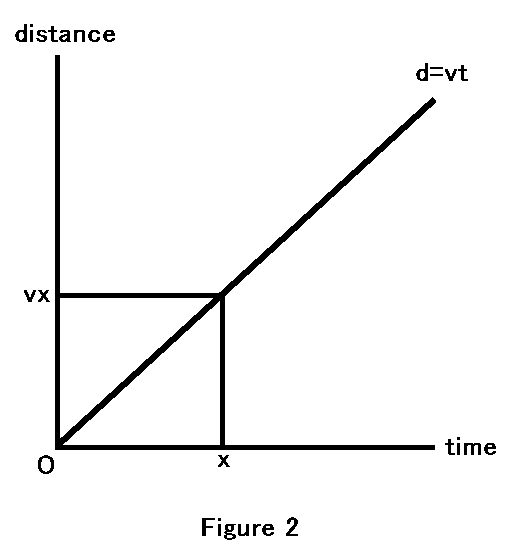
The position of the object at the time x is vx in the linear uniform motion of the speed v. So we can easily calculate the location of the object at any time. Because this modeling is advantageous for survival, our brain creates the uniform linear motion.
The arrow paradox is based on this model. Consider an instant. Because the length of time at an instant is zero, the object is stopping at an instant. Next, it expressed with the equation. If we substitute 0 into t in the equation d=vt, then d=0. All the same, the arrow is stopping.
Next, let us consider whether time consists of instants or not. No matter how many instants are collected, the total length of time is zero.
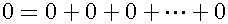
No matter how many zero are collected, the total value is zero. Furthermore, time is represented by the length of a line and an instant is represented by a point in the distance-time graph. No matter how many points are collected, the total length is zero. Hence, as I say in
Area Is Essential for Euclidean Geometry, the line doesn't consist of points. Therefore, time doesn't consist of instants. That is, the arrow paradox claims only the natural fact based on this model. However, the precondition, that time consists of instants, is wrong.
Where Is the Continuous World?
Our brain creates continuity for the modeling of the motion. However, inputs and outputs of our brain are
action potentials. They have the basic properties of Plato's one. As I say in
What Is the Natural Number One, the cognition of life is based on Plato's one. That is, continuity is made from digital data. This relationship is represented schematically in Figure 3.

Firstly, our eyes extract digital data from the real world. There is no continuity in the digital world. Secondly, our brain creates the analog world from the digital world. There are the continuous space and the continuous time and the instant in the analog world. Thirdly, human beings make mathematics from the analog world. Finally, scientists try to apply mathematics to the real world. This attempt has been successful beyond expectation. However, Zeno's paradoxes indicate that mathematics cannot necessarily apply to the real world.
References
- Zihl, J., Cramon, D. von, & Mai, N. 1983. Selective disturbance of movement vision after bilateral posterior brain damage. Brain, 106, 313-340. http://brain.oxfordjournals.org/content/106/2.toc
- Zihl, J., Cramon, D. von, Mai, N. & Schmid, C.H. 1991. Disturbance of movement vision after bilateral posterior brain damage: Further evidence and follow up observations. Brain, 114, 2235-2252. http://brain.oxfordjournals.org/content/114/5.toc
Table of Contents